Данный пост навеян главой “2.8.3. Расшифровка криптограм” из книги В.Д. Колдаева “Основы алгоритмизации и программирования”.
Напомним, что о теме Буквометики говорилось ранее.
Вкратце напомню, что суть задачи в решении ребуса, подобному этому:
MOTOR
+ FIAT
------
VOLVO
где вместо букв нужно подставить цифры, при этом две различные буквы должны иметь различный цифровой эквивалент.
Описание:
В предыдущем посте перебирались все размещения без повторений, после чего проверялась корректность получившегося набора.
Суть же рассматриваемого подхода заключается в том, что перебираться будут не все комбинации, а только те, которые удовлетворяют набору логических правил. О правилах речь пойдет ниже. Если набор цифровых эквивалентов удовлетворяет полному набору правил, то ребус корректен.
Рассмотрим текущий ребус.
Представим ребус в виде матрицы из трех строк, и столбцов, количество которых равно длине суммы. В первой строке хранится первое слагаемое, во второй – второе, в третье – сумма. Если имеется ведущий ноль(как например в FIAT), то храним ведущий пробел на первом месте.
Учитывая все вышесказанное, получаем матрицу
01234
0 [ MOTOR ]
1 [ _FIAT ]
2 [ VOLVO ]
символ ‘_’ соответствует пробелу.
Будем формировать правила при проходе по матрице сверху вниз, слева направо.
1) На букву M накладывается только одно ограничение – оно не может быть равным 0, и следовательно может принимать любое значение из интервала. [1,9]
2) Буква V однозначно получается из значения M и переноса, соответствующего 0-ому столбцу, который определяется из суммы O+F.
Следовательно если перенос(p[0]) равен нулю, тогда
2.1) V = M и O + F < 10
Если p[0] = 1, тогда
2.2) V = M + 1 и O + F >=10.
Здесь необходимо учесть тот факт, что на сумму O + F будет еще влиять перенос на первом столбце, поэтому правильно будет так:
2.1) V = M и O + F + p[1] < 10
2.2) V = M + 1 и O + F + p[1] >=10.
3) Буква O может принимать любые значения из интервала [0,9]
4) Буква F будет вычисляться из неравенства 2.1) или 2.2) в зависимости от значения переноса p[0] и равенства O+F=O
И т.д. до конца. Если на каком то этапе получается, что текущая буква не может иметь ни одного значения, значить необходимо поменять значения ранее стоящих букв, или значения переносов.
Реализация:
Удобно решать рекурсивно. При этом сама рекурсия будет иметь прототип: void rec(int row, int col, int prevCarry, int carry), где row и col – номера строки и столбца текущего элемента в матрице, а prevCarry и carry – значения переноса на предыдущем и текущем разрядах.
Правила, образующие неравенства удобно хранить в виде структуры:
- struct rule {
- // this + pair < 10, если prevCarry == 0
- // this + pair >=10, если prevCarry == 1
- char pair; // парный символ
- int prevCarry; // предыдущий перенос
- int carry; // текущий перенос
- };
* This source code was highlighted with Source Code Highlighter.А набор правил в виде рванной матрицы:
vector<vector<rule> > rules(256);
где значение буквы this определяется номер строки в рванной матрице правил.
Например рассмотрим правило, где фигирируют буквы A,O. prevCarry = 1, carry = 1.
Из представленных значений ясно, что A + O + carry >= 10. Правило занесем таким способом:
rules[‘A’].push_back(rule(‘0’,prevCarry,carry));
P.S: К сожалению не удалось зачесть эту реализацию на задаче 251.Футбол и математика из-за Memory Limit. Но от этого данный подход не теряет своей привлекательности по быстродействию.





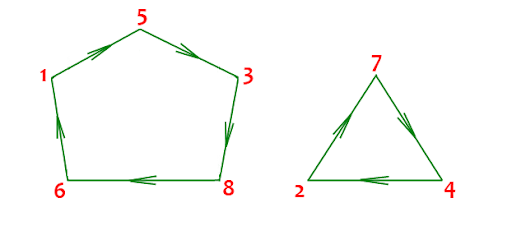
 Проделаем тоже самое для большого цикла [15386]. Здесь нам придется получить пятую степень перестановки.
Проделаем тоже самое для большого цикла [15386]. Здесь нам придется получить пятую степень перестановки.  Вопрос: Когда все 7 позиций “встанут” на свои места. Очевидно, когда первый цикл сделает 5 оборотов, а второй – 3. Следовательно нужно получить 15-ую степень исходной перестановки.
Вопрос: Когда все 7 позиций “встанут” на свои места. Очевидно, когда первый цикл сделает 5 оборотов, а второй – 3. Следовательно нужно получить 15-ую степень исходной перестановки. 



