Литература: Алгоритмы на С++. Роберт Седжвик
Организация биномиальных куч(очередей) имеет схожую природу с организацией хранения данных в виде массива куч, который мы использовали в реализации плавной сортировки, только здесь все проще.
Главное предназначение биномиальных куч в том, что их можно объединять за логарифмическое время. Как показывает практика такая задача практически не встречается в чистом виде, но зато может быть использована как подзадача в более сложной задаче.
Введем понятие Пирамидального дерева. Это двоичное дерево размером 2^N, в котором для каждого узла выполняется правило:
Все элементы левого поддерева не превышают значение текущего элемента.
Биномиальная куча содержит набор пирамидальных деревьев попарно различного размера.
Рассмотрим пример:
Известно, что биномиальная куча содержит 11 элементов. Это означает, что она состоит из 3 пирамидальных деревьев с размерами: 8, 2 и 1. Чтобы повторить эту операцию для произвольного размера биномиальной кучи необходимо представить этот размер в двоичном виде и взять степени двойки, соответствующие единичным битам в разложении. 11(10) = 1011(2) = 8 + 2 + 1.
Вот примеры правильных пирамидальных деревьев размером 1, 2, 4, 8:
- const int SIZE = 31;
- struct Node {
- int data;
- Node* left;
- Node* right;
- };
-
- struct binomial_queue {
- Node* mas[SIZE];
- int size;
- };
* This source code was highlighted with Source Code Highlighter.Сразу виден главный минус реализации биномиальной кучи. Это дополнительные 8 байтов, которые нужно тратиться для каждого элемента, чтобы иметь связь с правым и левым поддеревом.
Рассмотрим более подробно 5 операций:
2) Добавление элемента в биномиальную кучу
3) Поиск максимального элемента в биномиальной куче
4) Объединение двух биномиальных куч произвольного размера
5) Удаление максимального элемента из биномиальной кучи
1) Объединение двух пирамидальных деревьев в одну.
Сразу отметим тот факт, что объединять можно только пирамидальные деревья одинакового размера, т.к. только такое правило позволит получать в результате дерево размерностью 2^n. Рассмотрим два дерева размерностью 4:
В результате объединения получится дерево размерностью 8:
Объединение происходит по следующим правилам:
1) В корне результирующего дерева находится максимальный из корней исходных деревьев
2) Левое поддерево максимального корня становится правым поддеревом меньшего корня.
Как можно заметить для выполнения этой операции нужно просто грамотно переопределить ссылки:
- Node* join(Node* f, Node *s) {
- if (f->data > s->data) {
- s->right = f->left; f->left = s; return f;
- }
- else {
- f->right = s->left; s->left = f; return s;
- }
- }
* This source code was highlighted with Source Code Highlighter.В качестве параметров передаются указатель на корни двух объединяющихся деревьев. Результатом работы функции является указатель на корень объединенных деревьев.
2) Добавление элемента в биномиальную кучу
Эта операция полностью повторяет логику сложения двух двоичных чисел. Допустим нам нужно сложить 11 и 1.
1011
+ 0001
-------
1100
Единичный разряд будет переноситься до ближайшего справа нулевого бита. Функция добавления нового элемента может выглядеть вот так:
- void add(int val) {
- Node* newNode = new Node(val);
- Node* curNode = newNode;
- for (int i=0;i<SIZE;i++) {
- if (mas[i] == NULL) {
- mas[i] = curNode;
- break;
- }
- else {
- curNode = join(curNode,mas[i]);
- mas[i] = NULL;
- }
- }
- size++;
- }
* This source code was highlighted with Source Code Highlighter.3) Поиск максимального элемента в биномиальной куче
Корень каждого пирамидального дерева является максимальным элементов в данном дереве. Поэтому для поиска максимального элемента в биномиальной куче нужно последовательно перебрать все корни пирамидальных деревьев и выбрать максимальный.
4) Объединение двух биномиальных куч произвольного размера
Эта операция полностью повторяет процесс сложения двух двоичных чисел. При этом операнды и перенос при сложении принимают значения 0 или 1. Т.е. возникает 8 различных ситуаций. Касательно биномиальных куч эта операция может выглядеть вот так:
- void joinBQ(Node* a[], Node* b[SIZE]) {
- Node* c = 0;
- for (int i=0;i<SIZE;i++) {
- switch(num(c!=0,b[i]!=0,a[i]!=0)) {
- case 2: a[i] = b[i]; break;
- case 3: c = join(a[i],b[i]); a[i] = 0; break;
- case 4: a[i] = c; c = 0; break;
- case 5: c = join(a[i],c); a[i] = 0; break;
- case 6:
- case 7: c = join(b[i],c); break;
- }
- }
- }
- void joinBQ(binomial_queue &bq) {
- joinBQ(mas, bq.mas);
- size += bq.size;
- }
* This source code was highlighted with Source Code Highlighter.
5) Удаление максимального элемента из биномиальной кучи
Прежде чем удалить максимальный элемент из биномиальной кучи нужно найти его пирамидальное дерево, в котором он содержится, воспользовавшись п.2):
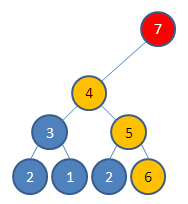
Исходное дерево содержит 8 узлов. После удаления корня пирамидального дерева останется три пирамидальных дерева размерностью 4,2 и 1: 
Эти деревья можно поместить во временную биномиальную кучу. После чего объединить её с текущей.
Все вышесказанное можно реализовать с помощью следующего кода:
- int getMax() {
- int res = 0;
- int resPos = -1;
- for (int i=0;i<SIZE;i++) {
- if (mas[i] && mas[i]->data > res) {
- res = mas[i]->data;
- resPos = i;
- }
- }
- Node** tmp = new Node*[SIZE];
- memset(tmp,0,sizeof(tmp)*SIZE);
- Node* cur = mas[resPos]->left;
- for (int i=resPos-1;i>=0;i--) {
- tmp[i] = new Node(*cur);
- cur = cur->right;
- tmp[i]->right = 0;
- }
- delete mas[resPos];
- mas[resPos] = 0;
-
- joinBQ(mas, tmp);
- delete tmp;
- size--;
- return res;
- }
* This source code was highlighted with Source Code Highlighter.Полная реализация находится: здесь
P.S: В ходе реализации возникла потребность создавать глубокую копию биномиальных куч, поэтому были дописаны конструкторы копирования для биномиальных куч и узлов пирамидальных деревьев.
